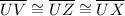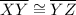Question

Given that point U is the circumcenter of triangle XVZ, which segments are congruent?

Answer 1

Answer:
`\overline{WX}\cong \overline{WV},\ \overline{VA}\cong\overline{AZ}`

`\overline{XY}\cong\overline{YZ}`

`\overline{UV}\cong \overline{UZ}\cong \overline{UX}`

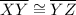
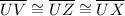
Explanation:

In the given figure we have a triangle , in which U is the circumcenter of triangle XVZ.

We know that the circumcenter is equidistant from each vertex of the triangle.

Since , the line segments which are representing the distance from the vertex and the circumcenter are
`\overline{UV},\ \overline{UZ},\ \overline{UX}`

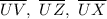
Also, The circumcenter is at the intersection of the perpendicular bisectors of the triangle's sides.

Then ,
`\overline{WX}\cong \overline{WV},\ \overline{VA}\cong\overline{AZ}` and
`\overline{XY}\cong\overline{YZ}`

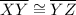
Hence, the segments which are congruent are
`\overline{UV}\cong \overline{UZ}\cong \overline{UX}`

`\overline{WX}\cong \overline{WV},\ \overline{VA}\cong\overline{AZ}`

`\overline{XY}\cong\overline{YZ}`

Answer 2

By definition, when we say congruent, this means that the segment or sides have exactly the same length or identical. Based on the given figure above given that point U is the circumcenter of triangle XVZ, the segments that are segment UW, segment UY, and segment UA. Also segment UV and segment UZ. Hope this answer helps.