What is the surface area of the cylinder with height 8 cm and radius 4 cm? Round your answer to the nearest thousandth.

Question

asked Apr 20, 2022 205k views

2 Answers

Moeabdol · Answer 1 · 2022-04-24T19:38:15+0000

Answer:

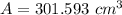
$A=301.593\ cm^3$

Explanation:

The Surface Area of a Cylinder

Given a cylinder of base radius r and height h, the surface area is calculated (including the top and bottom areas):

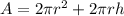
$A = 2\pi r^2+2\pi r h$

The cylinder has a height of h=8 cm and a radius of r=4 cm. Substituting:

$A = 2\pi 4^2+2\pi *4*8$

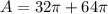
$A = 32\pi +64\pi$

$A=96\pi$

Calculating

$\boxed{A=301.593\ cm^3}$