Question

1. Two forces of 7 lb. and 14 lb. act on a body at right angles to each other. Find the angle their resultant force makes with the force of 14 lb.

2.A velocity of 30 mph is resolved into two components, each of which makes an angle of 45 with it. Find their magnitude.

Answer 1

1. 26.6°

2. 21.2 mph each

Step-by-step explanation:

1. When two forces are acting perpendicular to each other, then their resultant is given by:

R = √(F²+F'²+ 2 F F' cosθ) =√(7²+14²+ 2×7×14 cos 90°) = 15.65.

Angle between two vectors can be found using law of sines:

`(sin A)/(a)=(sin B)/(b)=(sin C)/(c)`

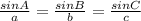
We have to find the angle (Ф) opposite side 7 lb force i.e. angle between Resultant and 14 lb force.

`(sin 90)/(15.65)=(sin \phi)/(7) \Rightarrow \phi = sin^(-1) (7)/(15.65) = 26.6^o`

2.

Let the components of velocity be v and v'

Because each component makes an angle 45° with the resultant, it can be found as:

v = 30 cos 45° = 21.2 mph

v' = 30 cos 45° = 21.2 mph

Both the components would be equal in magnitude.

Answer 2

1. The resultant force is equivalent to the hypotenuse of the triangle formed by the component forces, and the angle between the result and each component is found with trig based on that premise. You're looking for the angle formed by the hypotenuse and the longer of the two sides, so the larger component is used as the adjacent side and the smaller as the opposite side. So the angle is given by the inverse tangent of 7/14, or equivalently of 1/2.