Question

3^x : write in terms of base e and simplify! ...?

Answer 1

3^x : write in terms of base e would

3x=e^ln3^x

=e^xln3

Answer 2

The given function is exponential. Meanwhile
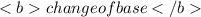
`<b>change of base</b>` has something to do with logarithms. So we convert the function to logarithm function, change to the required base and convert back to exponential function.

Let


`y = {3}^(x)`

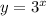
Writing the above exponential equation as a logarithmic equation, we obtain;


`log_(3)(y) = x`

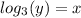
We can apply the change of base formula to obtain,


`( log_(e)(y) )/( log_(e)(3) ) = x`

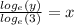
Or


`( ln(y) )/(ln(3) ) = x`

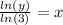
We can cross multiply to obtain;


`ln(y) = x ln(3)`

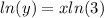
Taking logarithm of both sides to base e, we obtain;


`{e}^( ln(y) ) = {e}^(x ln(3) )`

This implies that,


`y= {e}^(x ln(3) )`
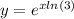
But we know that,

`y = {3}^(x)`
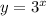
Hence

`{3}^(x) = {e}^(x ln(3))`