Question

Simplify

sqrt(3 + 2 sqrt 2) ...?

Answer 1

`1+√(2)`

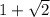
Explanation:

We have been given a radical expression
`\sqrt{3+2√(2)}`. We are asked to simplify the given expression.

We will add
`(√(2))^2-2` to our given expression as after adding and subtracting same quantity the value of our expression will be same.

`\sqrt{3+2√(2)+(√(2))^2-2}`

`\sqrt{3-2+2√(2)+(√(2))^2}`

`\sqrt{1+2√(2)+(√(2))^2}`

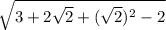
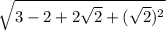
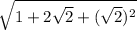
Using perfect square formula
`(a+b)^2=a^2+2ab+b^2` we can rewrite our expression as:

`\sqrt{1^2+2√(2)\cdot 1+(√(2))^2}`

`\sqrt{(1+√(2))^2}`

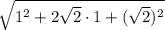
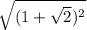
Applying radical rule
`\sqrt[n]{x^n} =x`, we will get,

`(1+√(2))^{(2)/(2)}=1+√(2)`

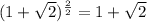
Therefore, the simplified form of our given expression would be
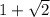`1+√(2)`.

Answer 2

The answer is 1 + √2

sqrt(2) is
`√(2)`
sqrt(3 + 2 sqrt 2) is
`\sqrt{3 +2 √(2) }`
Now, let's simplify
`\sqrt{3 +2 √(2) }`.
We will use square of sum: (a + b)² = a² + 2ab + b²


`\sqrt{3 +2 √(2) } = \sqrt{1+2+2 √(2) }= \sqrt{1+2 √(2)+2 }= \\ = \sqrt{1^(2) +2*1* √(2) + (√(2) ) ^(2) } = \sqrt{(1+ √(2)) ^(2)} =1+ √(2)`