Given data:
Mean: 41
Variance: 64
1. Find the standard deviation: the standard deviation is equal to the square root of the variance:
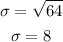
2. Find the z-score corresponding to a difference from the mean of 0.88:
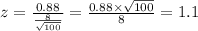
3. As the probability could be a mean 0.88 over the mean or 0.88 below the mean, Use a z-score table to find the value corresponding to z=1.1 and z=-1.1:
Find the probability between those z-score values:
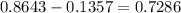
Then, the probability is 0.7286