Question

Consider the level surface given by

x2−y2+z2=2. Draw a picture for the following:

1. Slice for y=2
2. Slice for x=1
3. Slice for y=0
4. Slice for x=2 ...?

Answer 1

First of all, each slice represents an intersecting plane at that level.

For example, y = 2 is a plane that passes thorugh that level and cuts the volume given by
`x^(2) -y^(2)+z^(2)=2`

1. Slice for y = 2.

We replace this value in the given volume.

`x^(2) -y^(2)+z^(2)=2\\x^(2) -(2)^(2)+z^(2)=2\\x^(2)+z^(2)=2+4\\x^(2)+z^(2)=6`

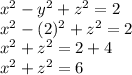
So, results in a circumference with radius
`√(6)`, because a circumference is defind as
`x^(2) +y^(2) =r^(2)`. (On plane XY).

2. Slice for x = 1.

We repeat the process.

`(1)^(2) -y^(2)+z^(2)=2\\z^(2)-y^(2)=2-1\\z^(2)-y^(2)=1`

It forms a horizontal hyperbola on plane ZY.

3. Slice for y = 0.

`x^(2) -0^(2)+z^(2)=2\\x^(2)+z^(2)=2`

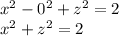
Another circle with radius of
`√(2)` on plane XZ.

4. Slice for x = 2.

`(2)^(2) -y^(2)+z^(2)=2\\z^(2)-y^(2)=2-4\\z^(2)-y^(2)=-2\\(z^(2)-y^(2))/(-2) =(-2)/(-2) \\(y^(2) )/(2) -(z^(2) )/(2) =1`

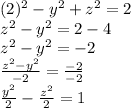
It forms a hyporbola on plane YZ.

Answer 2

1. circle of radius sqrt(6) in x-z plane 2. hyperbola in y-z plane opening in z direction3. circle of radius sqrt(2) in x-z plane 4. hyperbola in y-z plane opening in y direction