Question

For what value of c is the function defined below continuous on (-\infty,\infty)?

f(x) =
{x2−c2,X < 4 ; cx+20,x≥4.

Answer 1

`f(x)= \left \{ {{x^2-c^2,x \ \textless \ 4} \atop {cx+20},x \geq 4} \right`

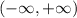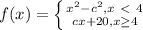
It's clear that for x not equal to 4 this function is continuous. So the only question is what happens at 4.
A function, f, is continuous at x = 4 if

`\lim_(x \rightarrow 4) \ f(x) = f(4)`

In notation we write respectively

`\lim_(x \rightarrow 4-) f(x) \ \ \ \text{ and } \ \ \ \lim_(x \rightarrow 4+) f(x)`

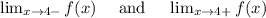
Now the second of these is easy, because for x > 4, f(x) = cx + 20. Hence limit as x --> 4+ (i.e., from above, from the right) of f(x) is just 4c + 20.

On the other hand, for x < 4, f(x) = x^2 - c^2. Hence

`\lim_(x \rightarrow 4-) f(x) = \lim_(x \rightarrow 4-) (x^2 - c^2) = 16 - c^2`

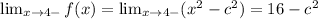
Thus these two limits, the one from above and below are equal if and only if
4c + 20 = 16 - c²
Or in other words, the limit as x --> 4 of f(x) exists if and only if
4c + 20 = 16 - c²


`c^2+4c+4=0 \\(c+2)^2=0 \\c=-2`

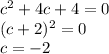
That is to say, if c = -2, f(x) is continuous at x = 4. Because f is continuous for all over values of x, it now follows that f is continuous for all real nubmers
`(-\infty, +\infty)`