We are given the following information;
Company A;
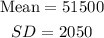
Comapny B;
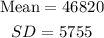
We have a normal distribution here. We can derive a standard normal distribution and the results would give us the z scores
That is;
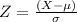
Therefore, if
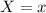
The z score would be;

However, in this case, the random variable is the target salary which is 55,000.
With X as the random variable we would have;
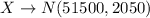
This is the tracking salary amount of employees in company A
Similarly;
With Y as the random variable we would have;

This on the other hand is the tracking salary amount of employees in company B.
If Jason's target is to get an annual salary of $55,000, the z score for company A would be;
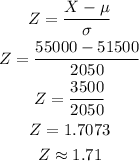
The z score for company B would be;
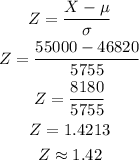
ANSWER:
The z scores for both companies are;
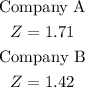
Both answers are rounded to 2 decimal places