Question

Suppose that Jason recently landed job offers at two companies. Company A reports an average salary of $51,500 with astandard deviation of $2,050. Company B reports an average salary of $46,820 with a standard deviation of $5,755. Assumethat salaries at each company are normally distributed.Jason's goal is to secure a position that pays $55,000 per year. What are the z-scores for Jason's desired salary at Company Aand Company B? Please round your answers to two decimal places.

Answer 1

We are given the following information;

Company A;

`\begin{gathered} \text{Mean}=51500 \\ SD=2050 \end{gathered}`

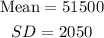
Comapny B;

`\begin{gathered} \text{Mean}=46820 \\ SD=5755 \end{gathered}`

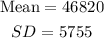
We have a normal distribution here. We can derive a standard normal distribution and the results would give us the z scores

That is;

`Z=((X-\mu))/(\sigma)`

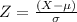
Therefore, if

`X=x`

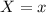
The z score would be;

`z=((x-\mu))/(\sigma)`

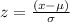
However, in this case, the random variable is the target salary which is 55,000.

With X as the random variable we would have;

`X\rightarrow N(51500,2050)`

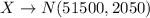
This is the tracking salary amount of employees in company A

Similarly;

With Y as the random variable we would have;

`Y\rightarrow N(46820,5755)`

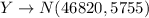
This on the other hand is the tracking salary amount of employees in company B.

If Jason's target is to get an annual salary of $55,000, the z score for company A would be;

`\begin{gathered} Z=(X-\mu)/(\sigma) \\ Z=(55000-51500)/(2050) \\ Z=(3500)/(2050) \\ Z=1.7073 \\ Z\approx1.71 \end{gathered}`

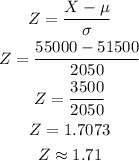
The z score for company B would be;

`\begin{gathered} Z=(X-\mu)/(\sigma) \\ Z=(55000-46820)/(5755) \\ Z=(8180)/(5755) \\ Z=1.4213 \\ Z\approx1.42 \end{gathered}`

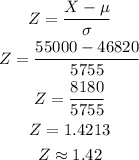
ANSWER:

The z scores for both companies are;

`\begin{gathered} \text{Company A} \\ Z=1.71 \\ \text{Company B} \\ Z=1.42 \end{gathered}`

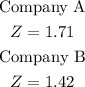
Both answers are rounded to 2 decimal places