Answer:
She need to drive more than 2000 miles for the first rental company to be a better deal .
Explanation:
Case 1) One car rental company offers a flat rate of $35 per day plus $0.10 per mile
Let m be the no. of miles
She will need the car for 5 days.
So, total cost =
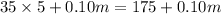
Case 2) Another car rental company offers the same car for $25 per day plus $0.25 per mile.
Let m be the no. of miles
She will need the car for 5 days.
So, total cost =

Now we are supposed to find How many miles would she need to drive for the first rental company to be a better deal?
So,
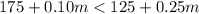

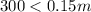
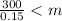
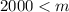
So, she need to drive more than 2000 miles for the first rental company to be a better deal