Answer:
1) 4.5% 2)1%
Explanation:
Given equation The monthly profits:
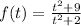
where t is in months after june 1st,2002
To find : The company's profits on June 1st, 2002
which means t=0
⇒

⇒

⇒

The company's profits on June 1st, 2002 = 4.5%
To find :The company's profits many years into the future
we take limit tends to infinity
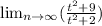

The company's profits many years into the future = 1%