Let x be the number of absences and y be the GPA
Given;
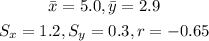
(a) The slope b of the lease squares regression line is;

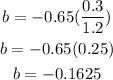
Hence, the slope is -0.1625
(b) The y-intercept of the line is;
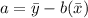
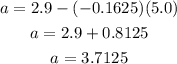
Hence, the y-intercept is 3.7125
(c) The equation of the line is;
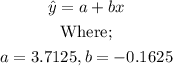
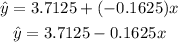
(d) The slope of the least-squares regression line is the average change in the predicted values of the response variable when the explanatory variable increases by 1 unit.
Hence, the slope of the least squares regression lines shows the change in the GPA due to number of absences.
(e) The estimate GPA for a student with three absences is;
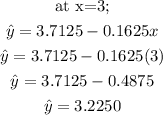
(f) The r-squared value of the data is;
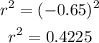
An r-squared of 42% shows that 42% of the data fit the regression model.