Question

Help??

Which of the following equations represents a parabola that opens up and has a vertex with a positive x-value?

A) y=-x^2+8x-15
B) y=2x^2-16x+38
C) y=2x^2+16x+24
D) y=-4x^2-14x-12

Answer 1

A parabola that opens up have a positive x∧2
So we know it can't be a or d so we are left with b or c
To find the x-value of the vertex, use the formula -b/2a
So the answer is B

Answer 2

option B

Explanation:

Find equations represents a parabola that opens up and has a vertex with a positive x-value

When leading term is positive then the parabola opens up.

When leading term is negative then the parabola opens down.

option A and D have leading term negative. so parabola opens down.

B)
`y=2x^2-16x+38`

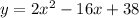
Now we find out the vertex using formula
`x=(-b)/(2a)`

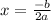
a=2 and b = -16

`x=(-b)/(2a)=(16)/(2(2))=4`

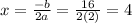
C)
`y=2x^2+16x+24`

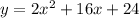
a=2 and b = 16

`x=(-b)/(2a)=(-16)/(2(2))=-4`

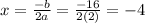
So option B represents a parabola that opens up and has a vertex with a positive x-value