We need to satisfy the following conditions:
1. The function is continuous on the closed interval [a,b]
2. f is differentiable on the open interval (a,b).
Let's check every condition:
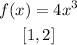
The function is continuous since there are no any restrictions.
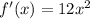
The derivative of the function exists over the interval (1,2)
Therefore:
Answer:
Yes, The mean value theorem can be applied
-----------------------
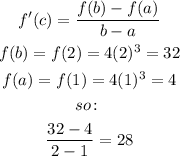
![\begin{gathered} f^(\prime)(c)=28 \\ 28=12x^2 \\ x^2=(28)/(12) \\ x=\sqrt[]{(7)/(3)} \\ \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/w9r3zjdtrk6ikjantl4z.png)
Therefore:
![undefined]()