Question

Matilda, Tanya and Renee are auditioning for a play. In how many ways can the girls fill the roles of a grandmother, mother, and daughter?

Would a permutation or combination be used to solve this problem?

Answer 1

Answer: 1) In 6 ways the girls can fill the roles of a grandmother, mother, and daughter.

2) A permutation would be used to solve this problem

Explanation:

Permutation is an arrangement of the elements of a list into a one to one correspondence with itself, where as a combination is a collection of things in which order doesn't matter at all.

In the given situation there are three girls named Matilda, Tanya and Renee are auditioning for a play. The girls have to fill the roles of a grandmother, mother, and daughter that means no girl can take two roles or no two girls can 1 role i.e. repetition is not allowed so by permutation ,

the number of ways the girls can fill the roles=
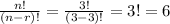`(n!)/((n-r)!)=(3!)/((3-3)!)=3!=6`,where n is the total roles and r is the number of girls.

Therefore, in 6 ways the girls can fill the roles of a grandmother, mother, and daughter.