Question

Determine which cross products are proportionate to each other. Select all situations that apply.

1/2 = 2/24
3/8y = 9/24y
4 = 64/16
x/y = y/x
3z/x = 9z/3x

Answer 1

3/8y = 9/24 since 3*3=9 and 8*3=24
4 = 64/16 since 16*4=64
3z/x = 9z/3x since 3z*3=9z and x*3=3x

Answer 2

Part 1)
`(1)/(2) =(2)/(24)`

`(2)/(24)` is
`(1)/(12)` in reduced form .

`(1)/(2) =(2)/(24)`

`(1)/(2)\\eq(1)/(12)`

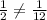
These are not proportionate to each other

Part 2)
`(3)/(8)y =(9)/(24)y`

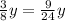
`(9)/(24)y` is
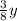`(3)/(8)y` in reduced form .

So,
`(3)/(8)y =(9)/(24)y`

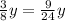
So, these are proportionate to each other .

Part 3)
`4 =(64)/(16)`

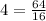
`(64)/(16)` is
`(4)/(1)` in reduced form .

So,
`4 =(64)/(16)`

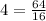
So, these are proportionate to each other .

Part 4)
`(x)/(y) =(y)/(x)`

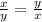
Since we cannot reduce
`(x)/(y)` into
`(y)/(x)` and vice versa.

So, These are not proportionate to each other

Part 5)
`(3z)/(x) =(9z)/(3x)`

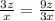
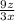`(9z)/(3x)` is
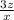`(3z)/(x)` in reduced form .

So,
`(3z)/(x) =(9z)/(3x)`

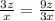
So, these are proportionate to each other .