Question

Which of the following is equal to the square root of the cube root of 5? 5 to the power of 1 over 3 5 to the power of 1 over 6 5 to the power of 2 over 3 5 to the power of 3 over 2

Answer 1

5 to the power 1/6

Explanation:

Answer 2

5 to the power of 1 over 6

or as an expression:
`5^{(1)/(6) }`

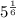
Explanation

First we are going to express our statement as an algebraic expression:

square root of the cube root of 5 =
`\sqrt{\sqrt[3]{5} }`

Next, we are using laws of radicals to simplify our expression:

Law of radicals:
`\sqrt[m]{\sqrt[n]{a} } =\sqrt[mn]{a}`

We can infer from our expression that n=2, m=3, and a=5, so lets replace the values:

`\sqrt{\sqrt[3]{5} }=\sqrt[(2)(3)]{5} =\sqrt[6]{5}`

Now, to express the radical as exponent, we are going to use another law of radicals:

Law of radicals:
`\sqrt[n]{a} =a^{(1)/(n) }`

Just like before, we can infer for our expression that n=6 and a=5, so let's replace the values:

`\sqrt[6]{5} =5^{(1)/(6) }`

And in words:

square root of the cube root of 5 is equal to 5 to the power of 1 over 6