Question

A uniform disk has a moment of inertia that is (1/2)MR2. A uniform disk of mass 13 kg, thickness 0.3 m, and radius 0.2 m is located at the origin, oriented with its axis along the y axis. It rotates clockwise around its axis when viewed from above (that is, you stand at a point on the +y axis and look toward the origin at the disk). The disk makes one complete rotation every 0.3 s.

What is the rotational angular momentum of the disk?

Answer 1

`L = 5.44 kg m^2/s`

Step-by-step explanation:

here we know that

mass of the disc is m = 13 kg

here we know that radius of disc = 0.2 m

now we have moment of inertia given as

`I = (1)/(2)mR^2`

`I = (1)/(2)(13 kg)(0.2)^2`

`I = 0.26 kg m^2`

now in order to find the angular momentum we know that

`L = I\omega`

`L = 0.26 * \omega`

here angular velocity is given by

`\omega = (2\pi)/(T)`

`\omega = (2\pi)/(0.3)`

`\omega = 21 rad/s`

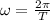
now angular momentum is given as

`L = 0.26 * 21 = 5.44 kg m^2/s`

Answer 2

The angular momentum of an object is equal to the product of its moment of inertia and angular velocity.
L = Iω
I = 1/2 MR²
I = 1/2 x 13 x (0.2)
I = 1.3

ω = 2π/t
ω = 2π/0.3
ω = 20.9

L = 1.3 x 20.9
= 27.2 kgm²/s