Question

What is the derivative of Sec^2(3x)

Answer 1

`\displaystyle y' = 6 \sec^2 (3x) \tan (3x)`

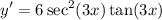
General Formulas and Concepts:

Calculus

Differentiation

• Derivatives
• Derivative Notation

Derivative Property [Multiplied Constant]:
`\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)`

Basic Power Rule:

1. f(x) = cxⁿ
2. f’(x) = c·nxⁿ⁻¹

Derivative Rule [Chain Rule]:
`\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

Explanation:

Step 1: Define

Identify

`\displaystyle y = \sec^2 (3x)`

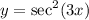
Step 2: Differentiate

1. Basic Power Rule [Derivative Rule - Chain Rule]:
   `\displaystyle y' = 2\sec (3x) \cdot [\sec (3x)]'`
2. Trigonometric Differentiation [Derivative Rule - Chain Rule]:
   `\displaystyle y' = 2\sec^2 (3x) \tan (3x) (3x)'`
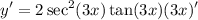
3. Basic Power Rule [Derivative Property - Multiplied Constant]:
   `\displaystyle y' = 6 \sec^2 (3x) \tan (3x)`

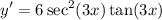
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Differentiation