Question

A bicyclist starting from rest applies a force of 346N to ride his bicycle across flat ground for a distance of 270m before encountering a hill making an angle of 29 degrees with respect to the horizontal. The bicycle and rider have a mass of 132kg combined. In this problem you can ignore air resistance and other losses did to friction. What is the bicycle’s speed, v in m/s just before the hill?

Answer 1

We are asked to determine the velocity of a bicycle when a force of 346 N is applied to it. To do that we will use a balance of energy.

The work applied to the bike is equivalent to the change in kinetic energy of the bicycle. Therefore, we have:

`W=(1)/(2)mv^2_f-(1)/(2)mv_0^2`

since the bicycle starts from rest this means that the initial velocity is zero:

`W=(1)/(2)mv_f^2`

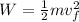
Since work is the product of force by distance we have:

`Fd=(1)/(2)mv^2`

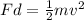
Where "F" is the force and "d" is the distance.

Now, we solve for the velocity. To do that we will multiply both sides by 2:

`2Fd=mv^2`

Now, we divide both sides by the mass:

`(2Fd)/(m)=v^2`

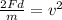
Now, we take the square root to both sides:

`\sqrt{(2Fd)/(m)}=v`

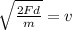
Now, we substitute the values:

`\sqrt{(2(346N)(270m))/(132kg)}=v`

Solving the operations:

`37.6(m)/(s)=v`

Therefore, the velocity is 37.6 meters per second.