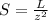Question

The volumes of two similar solids are 729 m3 and 125 m3. The surface area of the larger solid is 324 m2. What is the surface area of the smaller solid?

A) 56 m2
B) 100 m2
C) 500 m2
D) 200 m2

Answer 1

The correct answer is option B): "100 m2" because:

the ratio of the two solid is 729/125
the ratio of the surface area = (729/125)^(2/3)=81/25
surface area = 25 * 324 / 81 = 100 m 2

Answer 2

Option B

`100\ m^(2)`

Explanation:

Step 1

Find the scale factor

Let

z-----> scale factor

x-----> the volume of the larger solid

y-----> the volume of the smaller solid

we know that

The scale factor elevated to the cube is equal to the volume of the larger solid divided by the volume of the smaller solid

so

`z^(3)=(x)/(y)`

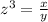
In this problem we have

`x=729\ m^(3), y=125\ m^(3)`

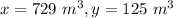
substitute

`z^(3)=(729)/(125)`

`z^(3)=5.832`

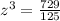
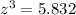
`z=1.8` ------> scale factor

Step 2

Find the surface area of the smaller solid

Let

z-----> scale factor

L-----> the surface area of the larger solid

S-----> the surface area of the smaller solid

we know that

The scale factor squared is equal to the surface area of the larger solid divided by the surface area of the smaller solid

so

`z^(2)=(L)/(S)`

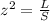
In this problem we have

`z=1.8, L=324\ m^(2)`

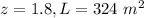
Substitute and solve for S

`S=(L)/(z^(2))`

`S=(324)/(1.8^(2))`

`S=100\ m^(2)`