Question

The time it takes to lay a sidewalk of a certain type varies directly as the length and inversely as the number of men working. If eight men take two days to lay 100 feet, how long will three men take to lay 150 feet?

Answer 1

just assume it as
8 men -> 2 days -- 100 feet
8 men -> 1 day -- 50 feet
1 man -> 1 day 50/8 feet
3 men -> 1 day 3*50/8 feet
so by doing so you'll get your answer which is 8 days

Answer 2

8 days

Explanation:

Direct Variation takes the form
`A=kB` , and

Inverse Variation takes the form
`A=k((1)/(B))`

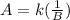
Where

• 
  `A` and
  `B` are the 2 variables associated, and
• 
  `k` is the proportionality constant

From the statement of the problem given, and taking time as
`t` and length as
`l` and number of men working as
`n`

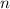
We can write:

`t=(kl)/(n)`

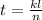
Using the values given in the problem (
`t=2` ,
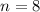`n=8` , and
`l=100` ), we can solve for k:

`2=((k)(100))/(8)\\16=k*100\\k=(16)/(100)=0.16`

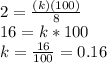
Now, we want to know time given
`n=3` and
`l=150` and
`k=0.16`

`t=((0.16)(150))/(3)\\3t=(0.16)(150)\\3t=24\\t=(24)/(3)\\t=8`

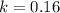
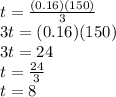
So, it will take 8 days.