Question

The length of a rectangle is 2 more than three times the width. The area of the rectangle is 161 square inches. What are the dimensions of the rectangle?

If x = the width of the rectangle, which of the following equations is used in the process of solving this problem?

2x^2 + 3x - 161 = 0
3x^2 + 2x - 161 = 0
6x^2 - 161 = 0

Answer 1

Answer: The answer is (B)
`3x^2+2x-161=0.`

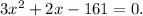
Step-by-step explanation: Given that 'x' represents the width of the rectangle.

According to the given information, the length of a rectangle is 2 more than three times the width. Therefore, the length of the rectangle is (3x + 2).

Hence, the area of the rectangle will be

`A=x(3x+2).`

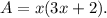
Since area of the rectangle is 161 square inches, so the equation is

`x(3x+2)=161\\\\\Rightarrow 3x^2+2x-161=0.`

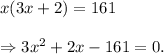
Solving the above equation, we find

`3x^2+2x-161=0\\\\\Rightarrow 3x^2+23x-21x-161=0\\\\\Rightarrow x(3x+23)-21(3x+23)=0\\\\\Rightarrow (x-21)(3x+23)=0\\\\\Rightarrow x-21=0,~~~~~3x+23=0\\\\\Rightarrow x=21,~~~~~~~~\Rightarrow x=-(23)/(2).`

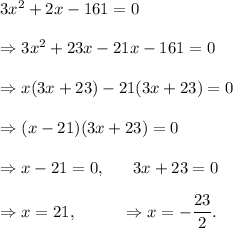
Since the width of the rectangle cannot be negative, so x = 21 inches.

And, length will be (3 × 21 +2) = 65 inches.

Thus, the length and width of the rectangle are 65 inches and 21 inches respectively.

And the correct equation is (B).