Question

1.Which of these is equivalent to the function g(x) = -|2x+4|+ 3?A g(x) = -(2x + 4) + 3B g(x) =2x + 7, x < -21-2x -1, x 2-2C g(x) = <3- 2x – 1, x < -22x + 7, x 2-2D g(x) ={-(2x + 4) + 3, x < 0(2x + 4) +3, x-20Illuminate Education™ Inc.

Answer 1

Given the function

`g(x)=-|2x+4|+3`

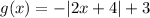
The expressions are equivalent if they show the same result as the original one.

A.

`g(x)=-(2x+4)+3`

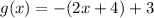
Since the terms held by the | | are positive, one solving the multiplication by -1 they will be negative with or without the module. This means that this expression is equivalent. (Alsmos the same just changed the module lines by parenthesis)

B.

`g(x)\left\{ \begin{aligned}2x+7,\text{ x<-2} \\ 1-2x-1,\text{ x2-2}\end{aligned}\right.`

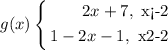
C.

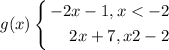
`g(x)\left\{ \begin{aligned}-2x-1,x<-2 \\ 2x+7,x2-2\end{aligned}\right.`

D.

`g(x)\left\{ \begin{aligned}-(2x+4)+3,x<0 \\ (2x+3)+3,x-20\end{aligned}\right.`

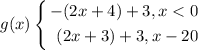
For the expressions that you posted, only A is equivalent.