Question

Find the value of k. The diagram is not drawn to scale.

Answer 1

The angles of a triangle must all equal 180, so 62+45=107. Then you take 107 from 180 which is 180-107=73 So k= 73

Answer 2

Answer: The value of k is 73.

Step-by-step explanation:

In the give diagram mark the corner points as A, B and C same as figure shown below.

From the figure it is noticed that,

`\angle A=62^(\circ)`

`\angle B=45^(\circ)`

`\angle C=k^(\circ)`

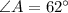
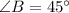
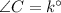
According to the angle sum property of triangle the sum of interior angles of a triangle is
`180^(\circ)`.

By the angle sum property of triangle we can say that,

`\angle A+\angle B+\angle C=180^(\circ)`

`62^(\circ)+45^(\circ)+k^(\circ)=180^(\circ)`

`107^(\circ)+k^(\circ)=180^(\circ)`

`k^(\circ)=180^(\circ)-107^(\circ)`

`k^(\circ)=73^(\circ)`

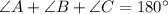
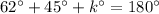
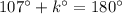
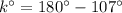
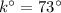
Therefore, the value of k is 73.