Question

Please please help! Rita and Chris are making patterns out of tiles. The first 4 figures in each of their patterns is shown.Continuing these patterns, Is there a figure for which the number of tiles in Rita's figure will be the sameas the number of tiles in Chris's figure? If so, what is the figure number, and how many tiles will be in eachfigure? Complete the explanation.Rita's PatternChris's Pattern1y =Rita'sThe system of equations for Rita's and Chris's patterns isy =Chris's .This system ofequations has the solution (). The number of tiles in Rita's and Chris's figures(select) be equal, because the number of tiles cannot be (select) and the figure number cannotbe a (select)

Answer 1

1. From the picture above, checking the number of tiles, we will notice that Rita's tiles combination is adding by 4, while Chris' pattern of tiles is adding by 6

Hence, the equation for Rita's pattern is y = 1 + 4n

And the Equation for Chris' pattern is y = 2 + 6n, where n is the number of tiles in both cases

2. This system of Equation has the solution?

we will equate both equations, that is y = 1 + 4n and 2 + 6n to find n and y.

`\begin{gathered} \text{Therefore, 1 + 4n = 2 + 6n} \\ 1\text{ -2 = 6n - 4n } \\ -1\text{ = 2n} \\ 2n\text{ = -1} \\ n\text{ = }(-1)/(2) \end{gathered}`

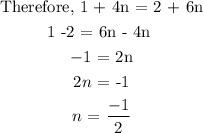
To find y, we put n = -1/2 into any of the equations.

`\begin{gathered} \text{From y = 1 + 4n } \\ y\text{ = 1 + 4(}(-1)/(2)) \\ y\text{ = 1 - }(4)/(2) \\ y\text{ = 1 - 2} \\ y\text{ = -1} \end{gathered}`

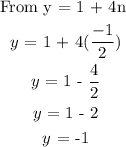
This system of Equation has the solution (n = -1/2, y = -1)

3. The number of tiles in Rita's and Chris's figures "cannot" be equal, because the number of tiles cannot be a negatve number and the figure number cannot be a fraction