Question

Use the remainder theorem to find P (3) for P(x) = -x+3x² - 2x-5.Specifically, give the quotient and the remainder for the associated division and the value of P(3).믐Quotient =Х5 ?Remainder = 0p(3) = 0

Answer 1

We are given the function

`P(x)=-x^3+3x^2-2x-5`

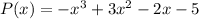
we are to use remainders theorem to find p(3)

Therefore

Given p(3) then x = 3

Hence

`\begin{gathered} P(3)=-3^3+3(3)^2_{}-2(3)-5 \\ P(3)=-27+27-6-5 \\ P(3)\text{ = -11} \end{gathered}`

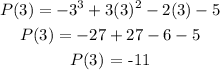
Hence, p(3) = - 11

Therefore, the Remainder is - 11

Finding the quotient

Given

`\begin{gathered} p(x)\text{ = 3 }\Rightarrow\text{ x = 3} \\ \text{therefore} \\ x\text{ -3 is a factor} \end{gathered}`

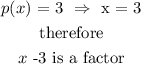
Therefore to find the quotient we will use long division method

`x-3\sqrt[]{-x^3+3x^(^2)-2x-5}`

This gives

`\begin{gathered} \text{ -x}^2\text{ -2} \\ x-3\sqrt[]{-x^3+3x^2-2x-5} \\ \text{ (-) -}x^3+3x^2 \\ ----------------------- \\ \text{ -2x - 5 } \\ \text{ ( - ) -2x}^{}\text{ + 6} \\ -------------------- \\ \text{ - 11} \end{gathered}`

Therefore, The quotient is

`-x^2-2`

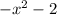
From the solution above

P(3) = - 11