The triangle inequality says that in any triangle, the sum of any two sides is always greater than the third side.
In other words,
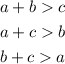
Now in our case, two sides are given and if we call a = 26m and b = 48m, the above gives
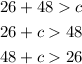
which solve for c to give
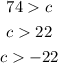
Now, between c>22 and c> -22, the inequality c> 22 encompasses everything and so we disregard c> -22 and choose c> 22; hence, we have
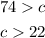
this says c is less than 74 but greater than 22, meaning
[tex]22mwhich is our answer!