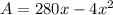Question

These 2 questions I need background/reasoning on every step of answer as I’ve never done this problem before.

Answer 1

Given:

The length of the rectangle ABCD (in metres)=

`l=2x`

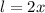
Breadth of the rectangle ABCD (in metres)=

`b=y`

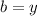
Perimeter of the rectangle ABCD (in metres)=

`280\text{ }`

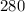
Required:

(1) To show that the area A, of the rectangle can be written as:

`A=280x-4x^2`

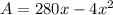
(2) Maximum possible area that the rectangle can occupy.

Answer:

(1) We know that the perimeter(P) of the rectangle is,

`P=2(l+b)`

Therefore, substituting values, we get,

`\begin{gathered} P=2(l+b) \\ 280=2(2x+y) \\ (280)/(2)=2x+y \\ 140=2x+y \\ y=140-2x \end{gathered}`

Now, we know that the area(A) of the rectangle is,

`A=l* b`

Therefore, substituting values, we get,

`\begin{gathered} A=l* b \\ A=2x* y \\ A=2x*(140-2x) \\ A=(2x*140)-(2x*2x) \\ A=280x-4x^2 \end{gathered}`

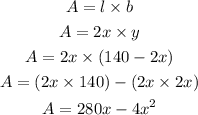
Hence, the area A, of the rectangle can be written as:

`A=280x-4x^2`

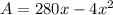
(2) The maximum possible area that the rectangle can occupy is,

`\begin{gathered} A=l* b \\ A=2x* y \\ A=2x*(140-2x) \\ A=(2x*140)-(2x*2x) \\ A=280x-4x^2 \end{gathered}`

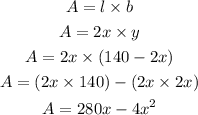
Hence, the maximum possible area of the rectangle is,

`A=280x-4x^2`

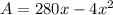
Final Answer:

The area A, of the rectangle can be written as:

`A=280x-4x^2`

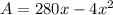
The maximum possible area of the rectangle is,

`A=280x-4x^2`