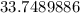Solution:
Given that an 18-foot ladder leans against a wall so that the base of the ladder is 10 feet from the base of the building, we can illustrate this in a diagram as shown below:
where

To evaluate the angle the ladder makes with the building, we use trigonometric ratio.
From trigonometric ratios:
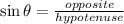
In this case,
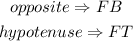
Thus, we have
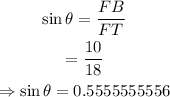
Take the sine inverse of both sides,
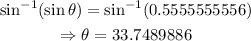
Hence, the angle the ladder makes with the building is