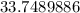Question

An 18-foot ladder leans against a wall so that the base of the ladder is 10 feet from the base of the building. What angle does the ladder make with the building?

Answer 1

Given that an 18-foot ladder leans against a wall so that the base of the ladder is 10 feet from the base of the building, we can illustrate this in a diagram as shown below:

where

`\begin{gathered} FT\Rightarrow length\text{ of the ladder} \\ FB\Rightarrow distance\text{ from the base of the ladder to the wall} \\ \theta\Rightarrow angle\text{ the ladder makes with the building} \end{gathered}`

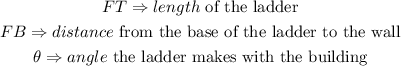
To evaluate the angle the ladder makes with the building, we use trigonometric ratio.

From trigonometric ratios:

`\sin\theta=(opposite)/(hypotenuse)`

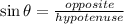
In this case,

`\begin{gathered} opposite\Rightarrow FB \\ hypotenuse\Rightarrow FT \end{gathered}`

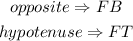
Thus, we have

`\begin{gathered} \sin\theta=(FB)/(FT) \\ =(10)/(18) \\ \Rightarrow\sin\theta=0.5555555556 \\ \end{gathered}`

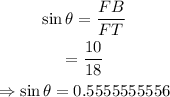
Take the sine inverse of both sides,

`\begin{gathered} \sin^(-1)(\sin\theta)=\sin^(-1)(0.5555555556) \\ \Rightarrow\theta=33.7489886\degree \end{gathered}`

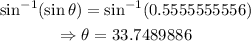
Hence, the angle the ladder makes with the building is

`\begin{equation*} 33.7489886\degree \end{equation*}`