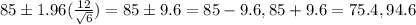Question

Data on the blood cholesterol levels of 6 rats give mean = 85, s= 12. A 95% confidence interval for the mean blood cholesterol of rats under this condition is

a)72.4 to 97.6
b)73.0 to 97.0
c)75.4 to 94.6
d)72.4 to 94.6

Answer 1

The equation of this would be


`true \ mean=mean \ +/- \ z(s)/( √(n) )`

The z-value for a 95% confidence level is equal to 1.96.

Then the lower limit would be:


`85-1.96 (12)/( √(6) )=75.398`

And the higher limit would be:


`85+1.96 (12)/( √(6) )=94.60`

Therefore, the answer is

c)75.4 to 94.6

I hope I was able to explain it clearly. Have a good day :)

Answer 2

The correct answer is:

c)75.4 to 94.6

Step-by-step explanation:

The formula for a confidence interval is:

`\mu \pm z*((\sigma)/(√(n)))`,

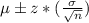where μ is the mean, z is the z-score associated with the level of confidence we want, σ is the standard deviation, and n is the sample size.

Our mean is 85, our standard deviation is 12, our sample size is 6, and since we want 95% confidence, our z-score is 1.96:

`85\pm 1.96((12)/(√(6)))=85\pm 9.6=85-9.6, 85+9.6=75.4, 94.6`