Question

The remain of an ancient ball court include a rectangular playing alley with a perimeter of about 72 m. The length of the alley is three times the width. Find the length and the width of the playing alley.The width is ?m and the length is ?m.

Answer 1

• Width: 9 m

,

• Length: 27 m.

Explanation:

Let the width of the alley = w.

The length of the alley is three times the width, therefore:

• The length of the alley = 3w

The perimeter of the alley = 72 m.

The perimeter of a rectangle is calculated using the formula:

`P=2(\text{Length}+\text{Width)}`

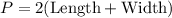
Substitute the values:

`72=2(3w+w)`

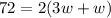
Solve the equation for w.

`\begin{gathered} \text{7}2=2(4w) \\ \text{7}2=8w \\ \text{Divide both sides by }8 \\ (72)/(8)=(8w)/(8) \\ w=9\; m \end{gathered}`

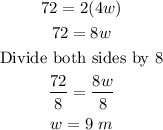
Finally, find the length of the alley.

`l=3w=3*9=27\; m`

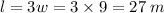
The width is 9 m and the length is 27 m.