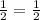Answer:
the answer is the option A
They are similar because Line BR : Line DB is
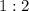 and line KE : Line YK
and line KE : Line YK
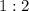
Explanation:
we know that
If the figures are similar
then
the ratio of their corresponding figures are equal
so
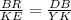
Find the distances
the formula to calculate the distance between two points is equal to

Find the distance BR
substitute the values



Find the distance KE
substitute the values



Find the distance DB
substitute the values



Find the distance YK
substitute the values



substitute
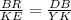
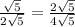
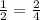
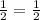 --------> the figures are similar
--------> the figures are similar
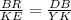 -----> rewrite
-----> rewrite
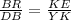
substitute the values
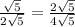
simplify
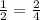 ------>
------>