Question

You are explaining why astronauts feel weightless while orbiting in the space shuttle. Your friends respond that they thought gravity was just a lot weaker up there. Convince them and yourself that it isn't so by calculating the acceleration of gravity 248 km above the Earth's surface in terms of g. (The mass of the Earth is 5.97 1024 kg, and the radius of the Earth is 6380 km.)

Answer 1

The acceleration of gravity at 248 km above the Earth's surface is
`9.08 m/s^2`.

Step-by-step explanation:

Mass of an object at 248 km above earth = m

Mass of earth = 5.97 1024 kg

Radius of the earth = 6380 km

Distance between earth and object,d= r + 248 km = 6628 km

Gravitational constant = G =
`6.674* 10^(-11) m^3/ kg s^2`

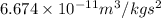
Gravitational force between object and earth:

`F'=G(Mm)/(d^2)`

Weight of the object at 248 km above earth : W

W' = mg'

W' = F'

`mg'=G(Mm)/(d^2)`

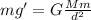
`g'=G(M)/(d^2)`.....[1]

Weight of the object on the surface of the earth:

W = mg

Gravitational force between on the surface earth:

`F=G(Mm)/(r^2)`

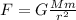
F = W

`g=G(M)/(r^2)`....[2]

Dividing [1] by [2]

`(g')/(g)=(G(M)/(d^2))/(G(M)/(r^2))=(r^2)/(d^2)`

`(g')/(g)=((6,380 km)^2)/((6,628 km)^2)=0.9267`

`g'=0.9267g = 0.9267* 9.8 m/s^2=9.08 m/s^2`

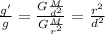
The acceleration of gravity at 248 km above the Earth's surface is
`9.08 m/s^2`.