We know that the initial frequency of the tires is 3 times per second, the frequency and angular velocity are related by:
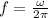
Then the initial angular velocity is:
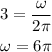
Now, we know that we stop at the end, that means that the final angular velocity is:

Now, since the angular acceleration is constant we can use the formula:
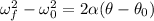
We know that the change in angular position is related to the change in linear position by:

where r is the radius of the motion. Then:
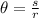
Hence the change in angular position in this problem is:
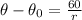
Then the angular accelaration is:
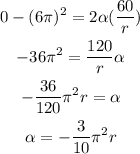
Therefore the angular accelaration is:
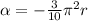
radians per second squared.
(We leave the answer is terms of the radius since we can't relate the angular motion with a linear motion in other way).