Question

What polynomial identity should be used to prove that 35 = 8 + 27

Answer 1

Sum of cubes

Explanation:

I just did the assignment

Answer 2

Sum of cubes identity should be used to prove 35 =3+27

Explanation:

Prove that : 35 = 8 +27

Polynomial identities are just equations that are true, but identities are particularly useful for showing the relationship between two apparently unrelated expressions.

Sum of the cubes identity:

`a^3+b^3=(a+b)(a^2-ab+b^2)`

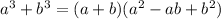
Take RHS

8+ 27

We can write 8 as
`2 * 2 * 2 = 2^3` and 27 as
`3 * 3 * 3 = 3^3`.

then;

8+27 =
`2^3+3^3`

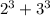
Now, use the sum of cubes identity;

here a =2 and b = 3

`2^3+3^3 = (2+3)(2^2-2\cdot 3+3^2)`

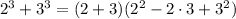
or

`2^3+3^3 = (5)(4-6+9)`
`= 5 \cdot 7 = 35` = LHS proved!

therefore, the Sum of cubes polynomial identity should be used to prove that 35 = 8 +27