The first step we need to do is substitute the value of 'b' in the expression of 'a':
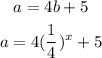
Now, we just need to apply the values of x given and find what is the least possible value of 'a':
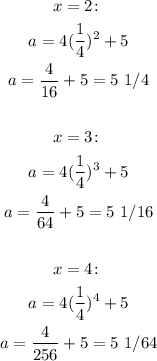
(x=2:
a = 4(1/4)^2 + 5
a = 4/16 + 5 = 5 1/4
x=3:
a = 4(1/4)^3 + 5
a = 4/64 + 5 = 5 1/16
x=4:
a = 4(1/4)^4 + 5
a = 4/256 + 5 = 5 1/64)
The least possible value of those 3 is the value a = 5 1/64
So the correct option is B.