To solve this, we need to propose two equations, one linear, and one quadratic.
We can propose:
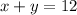
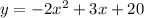
The system is:
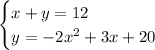
Now, we need to solve the system of equations. If we solve the first equation for y, then we can substitute in the second equation:
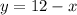
And substitute:
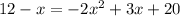
Next, we want to leave a '0' on one side of the equation:

We know how to find the solution to this equation, using the quadratic formula:
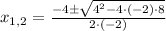
And solve:

Now, we can find the y-values of the solutions, using the first equation in the system:
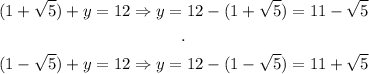
Thus, the two solutions to this system are:

And to verify, we can graph the system:
And see that our analytic result is correct.