Question

Find the dimension of a rectangle whose width is 10 miles less than its length and whose area is 75 square miles

Answer 1

w = L - 10
75 = L × ( L - 10 )
75 = L^2 - 10L
L^2 - 10L - 75 = 0
( L - 15 ) ( L + 5 ) = 0
L = 15

w = 15 - 10
w = 5

2 dimension

Answer 2

The length is 15 miles and the width is 5 miles.

Explanation:

The rectangle has two dimensions, width w and length l.

The area is given by the following formula:

`S = wl`.

In this problem, we have that:

The width is 10 miles less than its length. This means that

`w = l - 10`

The area is 75 square miles. So

`wl = 75`

`(l - 10)l = 75`

`l^(2) - 10l - 75 = 0`.

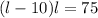
`l = 15` and
`l = -5`.

We cannot have negative dimensions. This means that the length is 15 miles and the width is 5 miles.