Question

Irina rode her bike to work at an average speed of 16 miles per hour. It started to rain, so she got a ride home along the same route in her coworker’s car at an average speed of 27 miles per hour. If Irina’s ride home in the car took 24 minutes (0.4 of an hour), how many hours was her bike ride to work, to the nearest tenth of an hour?

Answer 1

Two parts. First find the distance to work, second find the time to travel that distance by bike.
27 mph for .4 hours = 10.8 miles.
10.8 miles/16 mph = .675 hours
Rounded to the nearest tenth of an hour, .7 hours.

Therefore the solution is .7 hours.

Answer 2

0.7 hours

Explanation:

We know distance = rate * time, or
`D=rt`

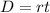
Since, the route is same, the Distance is same for both legs of the journey.

Let's call the first leg as
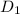`D_(1)` and second leg as
`D_(2)`

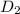
Therefore, using the distance formula above, we can write:

`r_(1)t_(1)=r_(2)t_(2)`

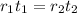
Substituting
`r_(1)=16` ,
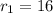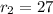`r_(2)=27` , and
`t_(2)=0.4` [given in the problem] into this equation and solving for
`t_(1)` gives us:

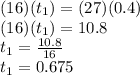`(16)(t_(1))=(27)(0.4)\\(16)(t_(1))=10.8\\t_(1)=(10.8)/(16)\\t_(1)=0.675` hours

Rounding to the nearest tenth of an hour, that is :

`0.7` hours