Question

Show from first principles that the derivative of a constant is zero

Answer 1

Given

To show from first principles that the derivative of a constant is zero .

Step-by-step explanation

We have to prove that from the first principle the derivative of a constant is zero.

To prove :

If f(x) =c, for some constant c, then f'(x) = 0.

Proof :

Suppose f(x) = c for some constant c.

Then the derivative of f(x) can be determined as

`\begin{gathered} f^(\prime)(x)=\lim_(h\to0)(f(x+h)-f(x))/(h) \\ f^(\prime)(x)=(c-c)/(h) \\ f^(\prime)(x)=0 \end{gathered}`

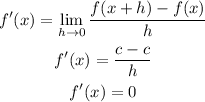
Hence proved.