Mean (μ): 1070 cc
Standard deviation (σ): 200 cc
(a)
We need to calculate the percentage of men that have a cranial capacity between 870 cc and 1270 cc.
Expressing 870 cc and 1270 cc in terms of the mean and the standard deviation leads to:

Then, this is equivalent to finding the percentage within one standard deviation from the mean. Using the 68-95-99.7 rule, this percentage is:

(b)
From the 68-95-99.7 rule, we know that 99.7% of the data in a normal distribution fall within 3 standard deviations from the mean. Then:
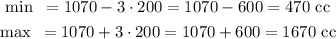
Answer:
Approximately 99.7% of men have cranial capacities between 470 cc and 1670 cc