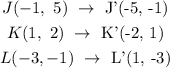The given points of the triangle JKL are:
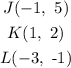
a. Reflection in the x-axis:
The rule for reflection in the x-axis is:
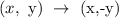
The reflection gives the points:
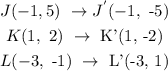
b. Translation along the vector <-2,4>:
Translation along the vector <-2, 4> gives the point:
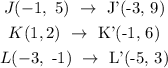
C. 90 degree counterclockwise rotation around the origin:
The rule for 90 degrees counterclockwise rotation:
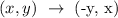
90 degree counterclockwise gives the point: