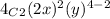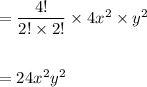Question

In two or more complete sentences, analyze how to find the third term in the expansion of (2x + y)4.

Answer 1

The first term in the binomial is "x2", the second term in "3", and the power n is 6, so, counting from0 to 6, the Binomial Theorem gives me:(x2 + 3)6 = 6C0 (x2)6(3)0 + 6C1(x2)5(3)1 + 6C2 (x2)4(3)2 + 6C3 (x2)3(3)3+ 6C4 (x2)2(3)4 + 6C5 (x2)1(3)5 + 6C6 (x2)0(3)6Then simplifying gives me(1)(x12)(1) + (6)(x10)(3) + (15)(x8)(9) + (20)(x6)(27)+ (15)(x4)(81) + (6)(x2)(243) + (1)(1)(729)= x12 + 18x10 + 135x8 + 540x6 + 1215x4 + 1458x2 + 729

Answer 2

The third term in the expansion of the given expression us:

`24x^2y^2`

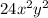
Explanation:

We are given an expression as:

`(2x+y)^4`

We know that by using the binomial theorem the expansion of the expression of the type:

`(ax+by)^n`

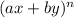
is given by:

`(ax+by)^n=n_C_0 (ax)^0(by)^(n-0)+n_C_1 (ax)^1(by)^(n-1)+...........+n_C_n (ax)^n(by)^(n-n)`

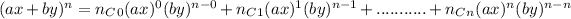
This means that there are n+1 terms in the expansion of the type:
`(ax+by)^n`

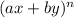
such that the rth term is:

`n_C_(r-1)* (ax)^(r-1)* (by)^(n-(r-1))`

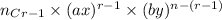
Here we have:

n=4,a=2 and b=1

Now, the third term in the expansion of the given expression is:

`4_C_2(2x)^2(y)^(4-2)`

`=(4!)/(2!* 2!)* 4x^2* y^2\\\\\\=24x^2y^2`