Question

A piece of gold with a mass of 15.23 g and an initial temperature of 54 °C was dropped into a calorimeter containing 28 g of water. The final temperature of the metal and water in the calorimeter was 62°C. What was the initial temperature of the water?

31.03 °C
62.13 °C
81.03°C
92.13°C

Answer 1

Answer:The initial temperature of the water 62.13 °C.

Step-by-step explanation:

Heat absorbed by the gold :Q

Mass of the gold ,m= 15.23 g

Specific heat capacity of gold = c = 0.129 J/g °C

Change in temperature of the gold =
`\Delta T`=62°C-54°C=8°C

Heat lost by the water : Q'

Mass of the water,m' = 28 g

Specif heat of water = c' = 4.179 J/g °C

Change in temperature of the water =
`\Delta T'`

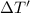
let the initial temperature of the water be T.

As per as Law of Conservation of Energy:

Q = -Q'

`m* c\Delta T=m'* c'* \Delta T'`

`15.23 g* 0.129 J/g ^oC* 8^oC=-(28 g* 4.179 J/g ^oC* \Delta T')`

`\Delta T'=-0.13^oC`

`-(0.13^oC)=(62^oC-T)`

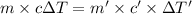
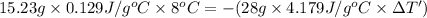
T = 62.13 °C

The initial temperature of the water 62.13 °C.

Answer 2

A piece of gold with a mass of 15.23 g and an initial temperature of 54 °C was dropped into a calorimeter containing 28 g of water. The final temperature of the metal and water in the calorimeter was 62°C. this can be solve using the formula H = mCpDeltaT where m is the mass, Cp is the heat capacity, delta T is the change in temperature

Cp of gold = 0.129 J/ g °C

Cp of water = 4.18 J/ g °C

The H for both are equal , so equate them and solve for the initial T of water

(15.23g) (0.129 J/ g C) (62 °C -54 °C) = (28 g)( 4.18 J/ g °C)( Ti –62 °C)

Ti = 62.13 °C