Question

1. State: ● domain and range ● x and y intercepts ● max and min values and where they occur ● period ● amplitude ● axis of symmetry ● values of a, k, d, and c for the sine function 2. Describe how this graph is related to the base function y=sin x by referring to horizontal and vertical shifts, amplitude, compressions or expansions, reflection

Answer 1

1)

Domain and range

Since the parent function is the sine function, the domain of the given graph has to consist of all the real numbers.

On the other hand, notice that the minimum value that the graph reaches is y=0, while the maximum y-value is 6; thus, the range of the function is [0,6].

The domain of the function is all real numbers and the range is [0,6].

x and y-intercepts

From the image, the y-intercept is (0,1.5), while there are multiple x-intercepts (-60,0), (300,0),... The x-intercepts are given by the formula

`(300\pm360n,0),n\rightarrow integer`

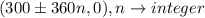
max and minimum values

As stated above, the minimum values of the function (or x-intercepts) are given by the expression (300+/-360n, 0).

As for the maximum values of the function, notice that the period of the graph is 360 (the distance between the two valleys is 360 units); then, the maximums of the functions are (120+/-360n, 6)

`\begin{gathered} minimum\rightarrow(300\pm360n,0) \\ maximum\rightarrow(120\pm360n,6) \\ n\rightarrow integer \end{gathered}`

Period.

Since the two valleys in the image are 360 units apart, the period of the function is 360 units

Amplitude.

The minimum value of the function is 0, while its maximum is 6; therefore, its amplitude is

`Amplitude=(6-0)/(2)=3`

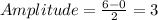
The amplitude is 3.

Axis of symmetry.

The axes of symmetry correspond to vertical lines on the plane that intersect the minimums and maximums of the function; then, The axes of symmetry are

`\begin{gathered} x=300\pm360n \\ and \\ x=120\pm360n \\ n\rightarrow integer \end{gathered}`

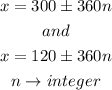
No information was provided about what a, k, d, and c are; therefore, this part of the question cannot be answered.

2.

The general form of a sine function is given below

`\begin{gathered} f(x)=Asin(B(x-C))+D \\ A\rightarrow amplitude \\ B\rightarrow period=(2\pi)/(B) \\ C\rightarrow\text{ horizontal shift} \\ D\rightarrow\text{ vertical shift} \end{gathered}`

Thus, in our case,

`\begin{gathered} A=3,B=(2\pi)/(360)=(\pi)/(180),C=-30,D=3 \\ \Rightarrow f(x)=3sin((\pi)/(180)(x-30))+3 \end{gathered}`

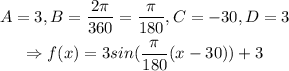
The graph of sin(x) is stretched vertically by a factor of 3, its amplitude is 3, its vertical shift is +3, its horizontal shift is -pi/6, its period is pi/180