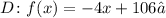number of patients at the given weeks:
week 5: 85 patients
week 10: 65 patients
We need to select a function from the options that, for a given week "x" we get an approximate to the number of patients that they had in those weeks.
One consideration is that the number of patients is decreasing:
week 5 is 85
and week 10 is 65.
What that means is that the function we choose, should have a negative number that accompanies the variable "x" to represent this decrese in patients.
Our two valid options are:
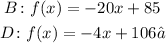
First we try option B. For 5 weeks x =5, and we get:
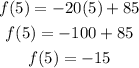
And since -15 is not even close to the number of patients on week 5, We discard this option.
Now we try option D, for week 5 (x=5), we get:
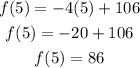
Which is really close to the number of patients on week 5.
We corroborate for week 10, x=10:
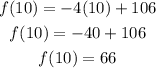
Which is also really close to the value for week 10.
Thus, our answer is: