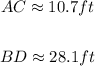Question

The sides of a parallelogram are 14ft and 16ft. One angle is 41° while another angle is 139°. Find the lengths of the diagonals of the parallelogram (to the nearest tenth of a foot).

Answer 1

We will have the following:

First, we have that the problem can be seeing as follows:

Now, knowing this and the the properties of the diagonals we will have that [We use the law of cosines}:

First diagonal [AC} is given by:

`\begin{gathered} AC=√(16^2+14^2-2cos(41))\Rightarrow AC=10.67193085... \\ \\ \Rightarrow AC\approx10.7 \end{gathered}`

So, one of the diagonals has an approximate length of 10.7 ft.

Second diagonal [BD] is given by:

`\begin{gathered} BD=√(16^2+14^2-2(16)(14)cos(139))\Rightarrow BD=28.10889347... \\ \\ \Rightarrow BD\approx28.1 \end{gathered}`

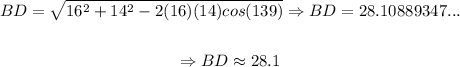
So, the second diagonal has a length of approximately 28.1 ft.

**Diagonals**

`\begin{gathered} AC\approx10.7ft \\ \\ BD\approx28.1ft \end{gathered}`